9.简单的Diff算法

vivien 2024/9/9 Vue

从暴力卸载再挂载，再到稍微优化（patch公共部分，剩余部分根据数组长短情况执行挂载或卸载），最后通过 diff 算法改进，一步步变得更好。

操作 DOM 的性能开销通常比较大，而渲染器的核心 Diff 算法就是为了解决这个问题而诞生的。

当新旧 vnode 的子节点都是一组节点时，为了以最小的性能开销完成更新操作，需要比较两组子节点，用于比较的算法就叫作 Diff 算法。

# 减少 DOM 操作的性能开销

直接使用 patch 函数去处理对应位置的新旧子节点，当它们类型一样时无需卸载重新挂载，还处理了新旧子节点长度不一样的情况。但这种思路处理不了不同类型子节点移动时的复用。

核心 Diff 只关心新旧虚拟节点都存在一组子节点的情况。在前面的学习中，我们针对两组子节点的更新，采用了一种简单直接的手段，即卸载全部旧子节点，再挂载全部新子节点。这么做的确可以完成更新，但由于没有复用任何 DOM 元素，所以会产生极大的性能开销。

 // 旧 vnode
 const oldVNode = {
   type: 'div',
   children: [
     { type: 'p', children: '1' },
     { type: 'p', children: '2' },
     { type: 'p', children: '3' }
   ]
 }
 // 新 vnode
 const newVNode = {
   type: 'div',
   children: [
     { type: 'p', children: '4' },
     { type: 'p', children: '5' },
     { type: 'p', children: '6' }
   ]
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

按照之前的做法，当更新子节点时，我们需要执行 6 次 DOM 操作：

卸载所有旧子节点，需要 3 次 DOM 删除操作；

挂载所有新子节点，需要 3 次 DOM 添加操作。

但是，通过观察上面新旧 vnode 的子节点，可以发现：

更新前后的所有子节点都是 p 标签，即标签元素不变；

只有 p 标签的子节点（文本节点）会发生变化。

最理想的更新方式是，直接更新这个 p 标签的文本节点的内容。这样，一共只需要 3 次 DOM 操作就可以完成全部节点的更新。相比原来需要执行 6 次 DOM 操作才能完成更新的方式，其性能提升了一倍。

按照这个思路，我们可以重新实现两组子节点的更新逻辑：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     // 重新实现两组子节点的更新方式
     // 新旧 children
     const oldChildren = n1.children
     const newChildren = n2.children
     // 遍历旧的 children
     for (let i = 0; i < oldChildren.length; i++) {
       // 调用 patch 函数逐个更新子节点
       patch(oldChildren[i], newChildren[i])
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

oldChildren 和 newChildren 分别是旧的一组子节点和新的一组子节点。我们遍历前者，并将两者中对应位置的节点分别传递给 patch 函数进行更新。patch 函数在执行更新时，发现新旧子节点只有文本内容不同，因此只会更新其文本节点的内容。这样，我们就成功地将 6 次 DOM 操作减少为 3 次。

整个更新过程的示意图如下：

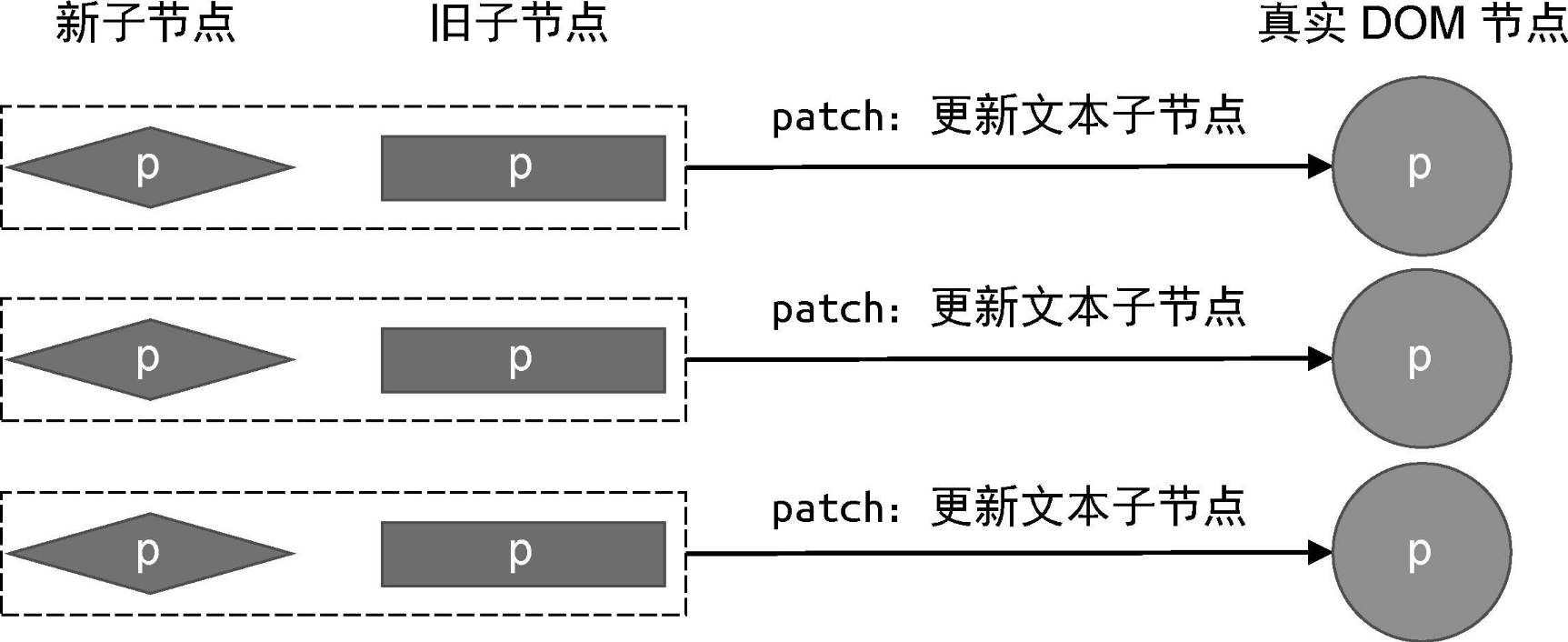
这种做法虽然能够减少 DOM 操作次数，但通过遍历旧的一组子节点，并假设新的一组子节点的数量与之相同，只有在这种情况下，这段代码才能正确地工作。但是，新旧两组子节点的数量未必相同。

当新的一组子节点的数量少于旧的一组子节点的数量时，意味着有些节点在更新后应该被卸载：

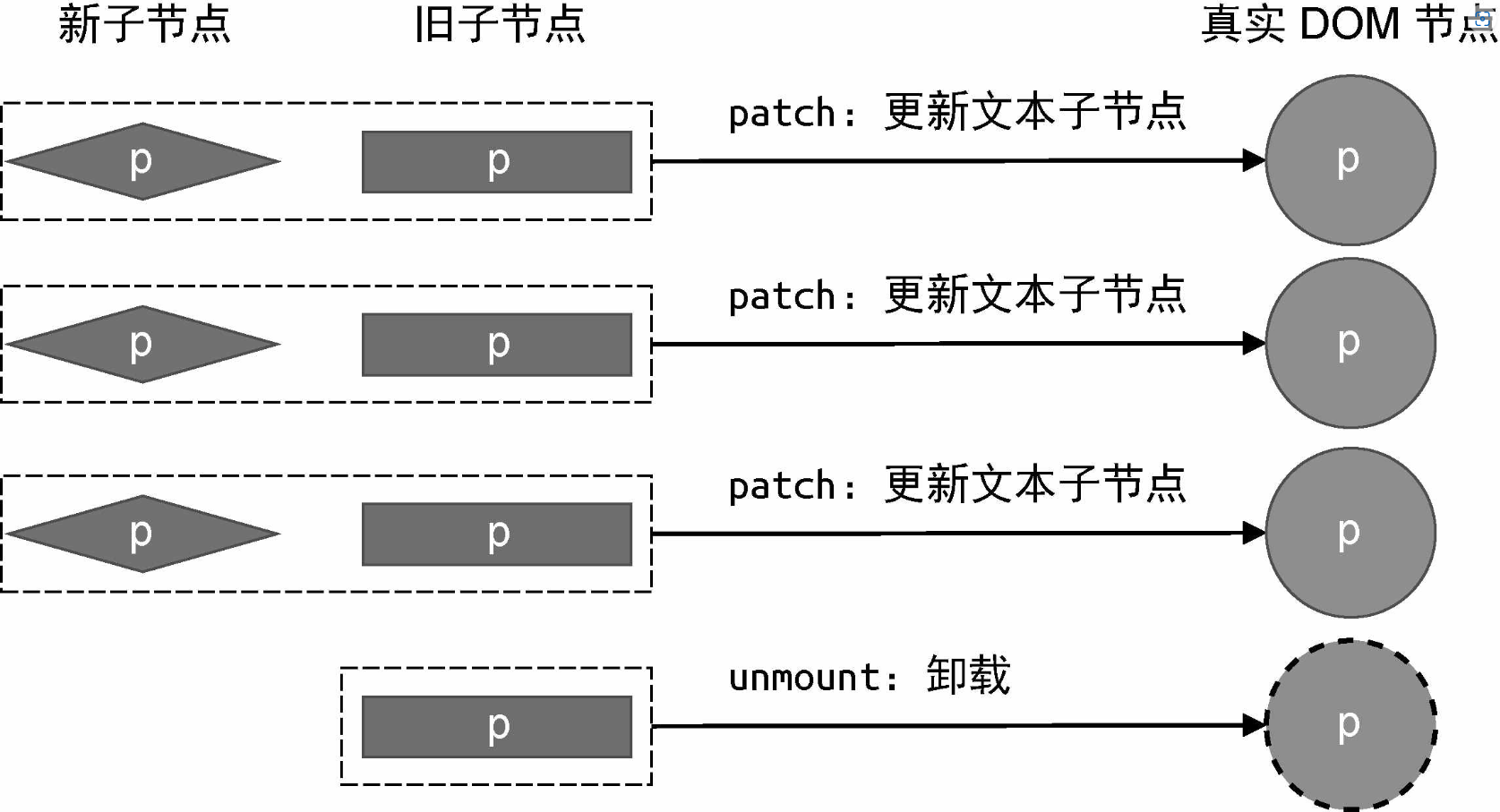
类似地，新的一组子节点的数量也可能比旧的一组子节点的数量多，意味着我们应该挂载新增节点：

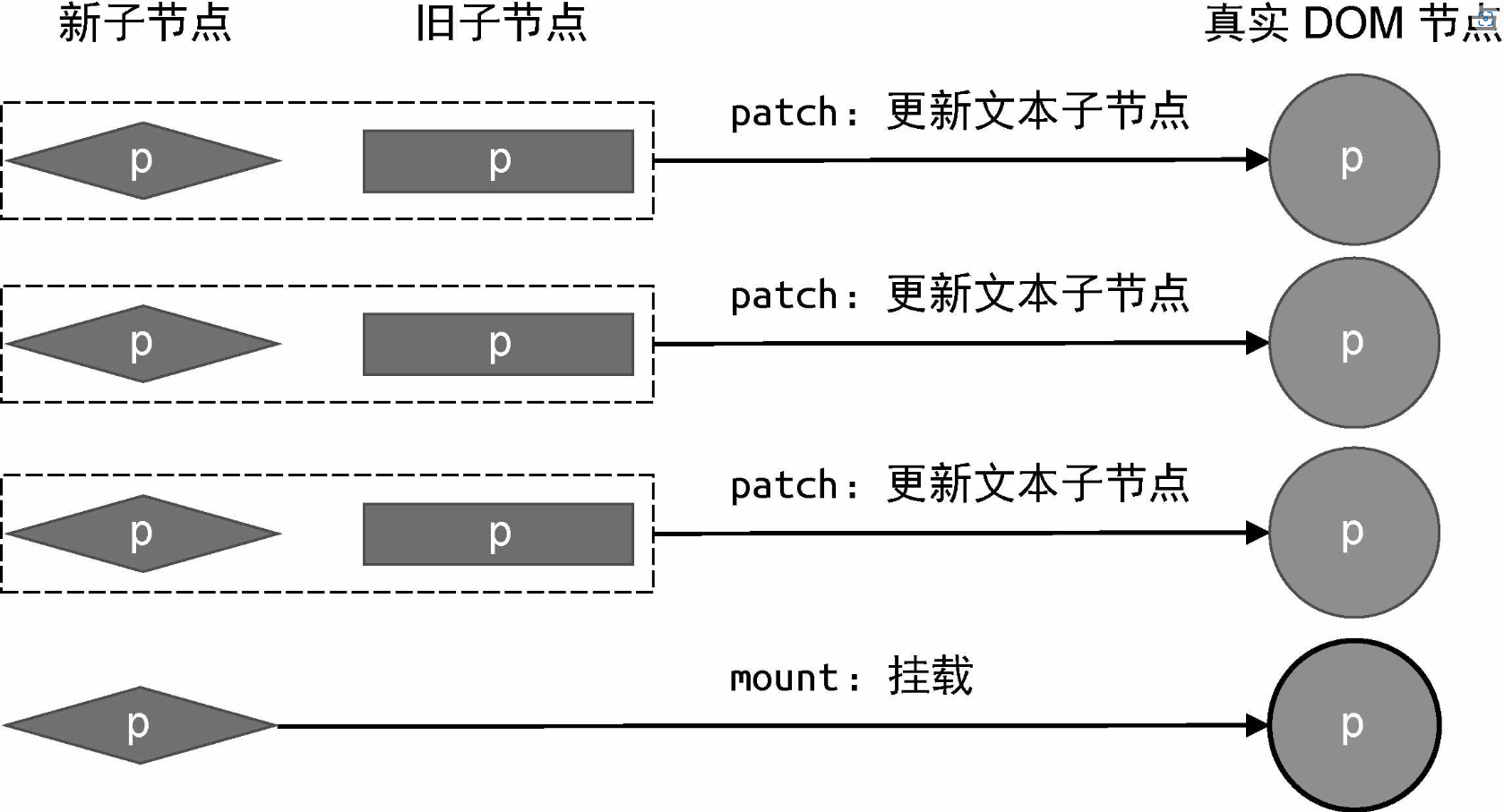
通过上面的分析我们意识到，在进行新旧两组子节点的更新时，不应该总是遍历旧的一组子节点或遍历新的一组子节点，而是应该遍历其中长度较短的那一组。这样，我们才能够尽可能少地调用 patch 函数进行更新。接着，再对比新旧两组子节点的长度，如果新的一组子节点更长，则说明有新子节点需要挂载，否则说明有旧子节点需要卸载。这样，无论新旧两组子节点的数量关系如何，渲染器都能够正确地挂载或卸载它们，最终实现如下：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     // 旧的一组子节点的长度
     const oldLen = oldChildren.length
     // 新的一组子节点的长度
     const newLen = newChildren.length
     // 两组子节点的公共长度，即两者中较短的那一组子节点的长度
     const commonLength = Math.min(oldLen, newLen)
     // 遍历 commonLength 次
     for (let i = 0; i < commonLength; i++) {
       patch(oldChildren[i], newChildren[i], container)
     }
     // 如果 newLen > oldLen，说明有新子节点需要挂载
     if (newLen > oldLen) {
       for (let i = commonLength; i < newLen; i++) {
         patch(null, newChildren[i], container)
       }
     } else if (oldLen > newLen) {
       // 如果 oldLen > newLen，说明有旧子节点需要卸载
       for (let i = commonLength; i < oldLen; i++) {
         unmount(oldChildren[i])
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

这种做法比暴力卸载再重新挂载性能要好一点。具体处理时，不考虑节点的移动，直接先在数量少的节点组上循环进行 patch 操作。然后判断新节点是不是比旧节点多，如果多，就在多的那部分上（其实就是末尾部分，因为没考虑 diff 移动）执行挂载操作；反之对旧节点未尾部分执行卸载操作。

# DOM 复用与 key 的作用

复用 DOM 元素省去了删除和创建的过程，但是仍需要 patch 操作。

patch 是在原有的节点上进行的，先通过 patch 更新节点内容，使得新旧节点内容保持一致，再通过移动节点位置完成更新操作。

前面，我们通过减少 DOM 操作的次数，提升了更新性能。但这种方式仍然存在可优化的空间。举个例子，假设新旧两组子节点的内容如下：

 // oldChildren
 [
   { type: 'p' },
   { type: 'div' },
   { type: 'span' }
 ]
 // newChildren
 [
   { type: 'span' },
   { type: 'p' },
   { type: 'div' }
 ]

1
2
3
4
5
6
7
8
9
10
11
12

如果使用上一节介绍的算法来完成上述两组子节点的更新，则需要 6 次 DOM 操作：

调用 patch 函数在旧子节点 { type: 'p' } 与新子节点 { type: 'span' } 之间打补丁，由于两者是不同的标签，所以 patch 函数会卸载 { type: 'p' }，然后再挂载 {type: 'span' }，这需要执行 2 次 DOM 操作。

与第 1 步类似，卸载旧子节点 { type: 'div' }，然后再挂载新子节点 { type: 'p'}，这也需要执行 2 次 DOM 操作。

与第 1 步类似，卸载旧子节点 { type: 'span' }，然后再挂载新子节点 { type:'div' }，同样需要执行 2 次 DOM 操作。

但是，观察新旧两组子节点，可以发现：二者只是顺序不同。

最优的处理方式是，通过 DOM 的移动来完成子节点的更新，这要比不断地执行子节点的卸载和挂载性能更好。

想要通过 DOM 的移动来完成更新，必须要保证一个前提：新旧两组子节点中的确存在可复用的节点。那么该如何确定新的子节点是否出现在旧的一组子节点呢？

一种答案是，通过 vnode.type 来判断，只要 vnode.type 的值相同，我们就认为两者是相同的节点。但这种方式并不可靠，例如：
// oldChildren
[
  { type: 'p', children: '1' },
  { type: 'p', children: '2' },
  { type: 'p', children: '3' }
]

// newChildren
[
  { type: 'p', children: '3' },
  { type: 'p', children: '1' },
  { type: 'p', children: '2' }
]
1
2
3
4
5
6
7
8
9
10
11
12
13
这两组子节点同样可以通过移动 DOM 的方式来完成更新。但所有节点的 vnode.type 属性值都相同，这导致无法确定新旧两组子节点中节点的对应关系，也就无法得知应该进行怎样的 DOM 移动才能完成更新。

因此，我们需要引入额外的 key 来作为 vnode 的标识，根据 key 来判断哪些 dom 子节点能够被复用，这样可以通过移动 dom 操作来代替增删 dom 完成子节点的更新，提高性能。

key 属性就像虚拟节点的“身份证”号，只要两个虚拟节点的 type 属性值和 key 属性值都相同，那么我们就认为它们是相同的，即可以进行 DOM 的复用：

 // oldChildren
 [
   { type: 'p', children: '1', key: 1 },
   { type: 'p', children: '2', key: 2 },
   { type: 'p', children: '3', key: 3 }
 ]
 // newChildren
 [
   { type: 'p', children: '3', key: 3 },
   { type: 'p', children: '1', key: 1 },
   { type: 'p', children: '2', key: 2 }
 ]

1
2
3
4
5
6
7
8
9
10
11
12

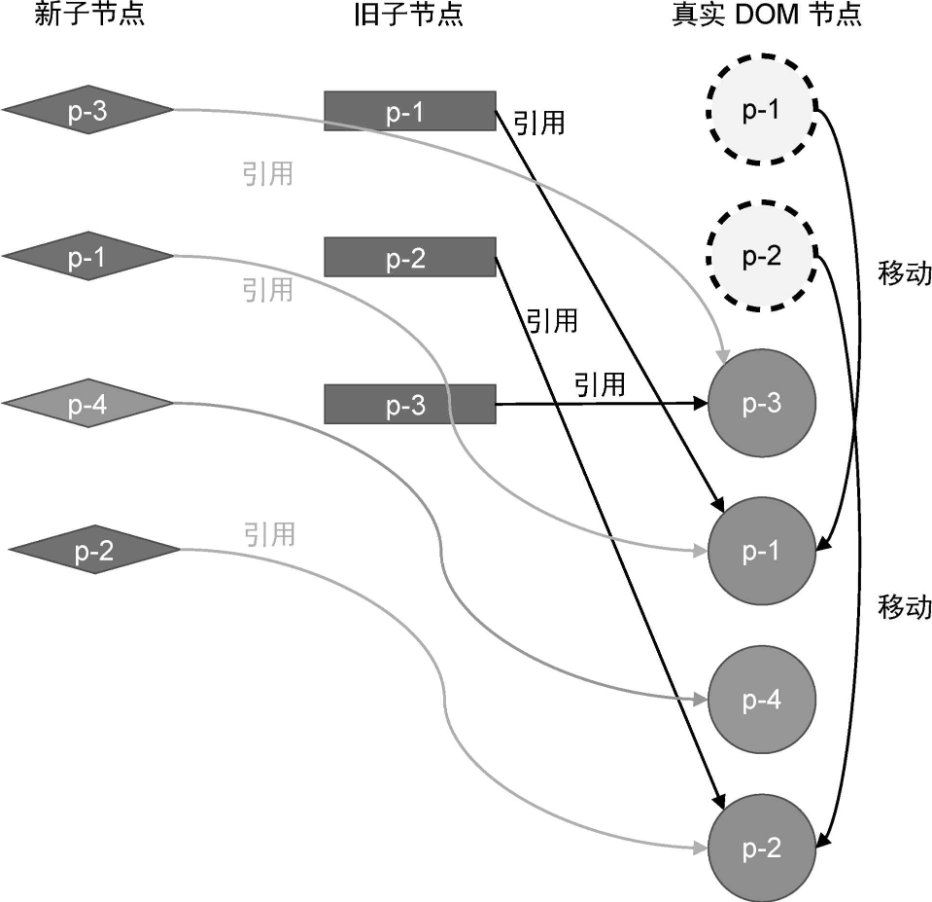
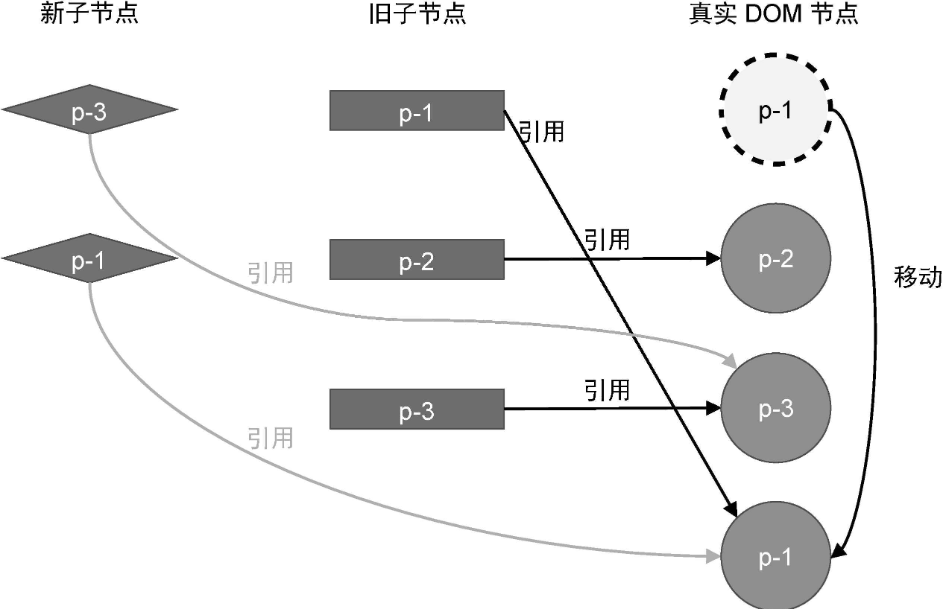
有 key 和无 key 时新旧两组子节点的映射情况如下：

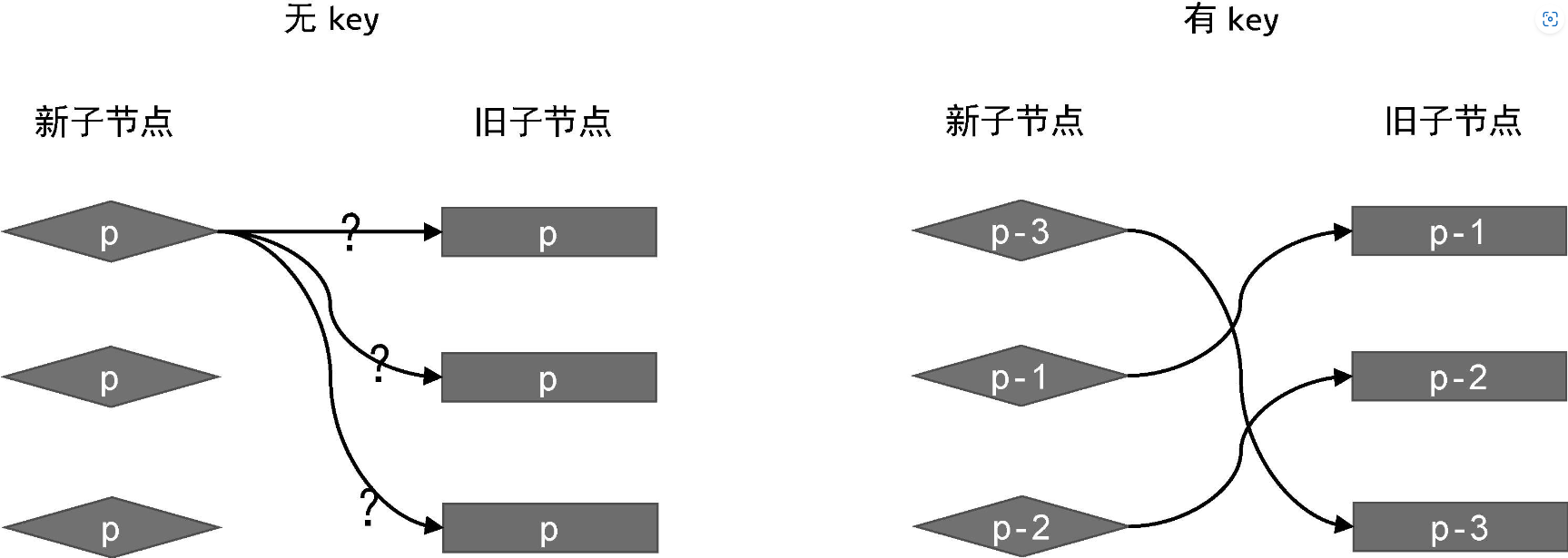
可见，如果没有 key，我们无法知道新子节点与旧子节点间的映射关系，也就无法知道应该如何移动节点。有 key 的话情况则不同，我们根据子节点的 key 属性，能够明确知道新子节点在旧子节点中的位置，这样就可以进行相应的 DOM 移动操作了。

在 Diff 算法中，我们根据 key 标识来得知每一个节点的位置，进而明确 DOM 节点移动的位置，而不是单纯地销毁和创建节点，最终达到节点复用的效果，提升整体性能。

注意！DOM 可复用并不意味着不需要更新，如下面的两个虚拟节点所示：

const oldVNode = { type: 'p', key: 1, children: 'text 1' }
const newVNode = { type: 'p', key: 1, children: 'text 2' }

1
2

这两个虚拟节点拥有相同的 key 值和 vnode.type 属性值。这意味着，在更新时可以复用 DOM 元素，即只需要通过移动操作来完成更新。但仍需要对这两个虚拟节点进行打补丁操作，因为新的虚拟节点（newVNode）的文本子节点的内容已经改变了（由 'text 1' 变成 'text 2'）。

因此，在讨论如何移动 DOM 之前，我们需要先完成打补丁操作：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     // 遍历新的 children
     for (let i = 0; i < newChildren.length; i++) {
       const newVNode = newChildren[i]
       // 遍历旧的 children
       for (let j = 0; j < oldChildren.length; j++) {
         const oldVNode = oldChildren[j]
         // 如果找到了具有相同 key 值的两个节点，说明可以复用，但仍然需要调用 patch 函数更新
         if (newVNode.key === oldVNode.key) {
           patch(oldVNode, newVNode, container)
           break // 这里需要 break
         }
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

使用了两层 for 循环，外层循环用于遍历新的一组子节点，内层循环则遍历旧的一组子节点。在内层循环中，逐个对比新旧子节点的 key 值，试图在旧的子节点中找到可复用的节点。一旦找到，则调用 patch 函数进行打补丁。

经过这一步操作之后，我们能够保证所有可复用的节点本身都已经更新完毕了。以下面的新旧两组子节点为例：

 const oldVNode = {
   type: 'div',
   children: [
     { type: 'p', children: '1', key: 1 },
     { type: 'p', children: '2', key: 2 },
     { type: 'p', children: 'hello', key: 3 }
   ]
 }
 const newVNode = {
   type: 'div',
   children: [
     { type: 'p', children: 'world', key: 3 },
     { type: 'p', children: '1', key: 1 },
     { type: 'p', children: '2', key: 2 }
   ]
 }
 // 首次挂载
 renderer.render(oldVNode, document.querySelector('#app'))
 setTimeout(() => {
   // 1 秒钟后更新
   renderer.render(newVNode, document.querySelector('#app'))
 }, 1000);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

1、取新的一组子节点中的第一个子节点，即 key 值为 3 的节点。尝试在旧的一组子节点中寻找具有相同 key 值的节点。发现，旧的子节点 oldVNode[2] 的 key 值为 3，于是调用 patch 函数进行打补丁。在这一步操作完成之后，渲染器会把 key 值为 3 的虚拟节点所对应的真实 DOM 的文本内容由字符串 'hello' 更新为字符串 'world'。

2、取新的一组子节点中的第二个子节点，即 key 值为 1 的节点。尝试在旧的一组子节点中寻找具有相同 key 值的节点。我们发现，旧的子节点 oldVNode[0] 的 key 值为 1，于是调用 patch 函数进行打补丁。由于 key 值等于1 的新旧子节点没有任何差异，所以什么都不会做。

3、取新的一组子节点中的最后一个子节点，即 key 值为 2 的节点，最终结果与第二步相同。

经过上述更新操作后，所有节点对应的真实 DOM 元素都更新完毕了。但真实 DOM 仍然保持旧的一组子节点的顺序，即 key 值为 3 的节点对应的真实 DOM仍然是最后一个子节点。

由于在新的一组子节点中，key 值为 3 的节点已经变为第一个子节点了，因此我们还需要通过移动节点来完成真实 DOM 顺序的更新。

# 找到需要移动的元素

判断索引是否非递增，非递增的元素要移动。简单来说，就是后一个的索引比前一个的要小就需要移动。

要不要移动看索引是否出现降序，怎么移是参照新节点数组中前一个节点，把当前节点的 el 移动到前个节点的 el 的后面。

现在，我们已经能够通过 key 值找到可复用的节点了。接下来需要思考的是，如何判断一个节点是否需要移动，以及如何移动。对于第一个问题的答案是，当新旧两组子节点的节点顺序不变时，就不需要额外的移动操作。

# 新旧子节点顺序不变

当新旧子节点顺序不变时：

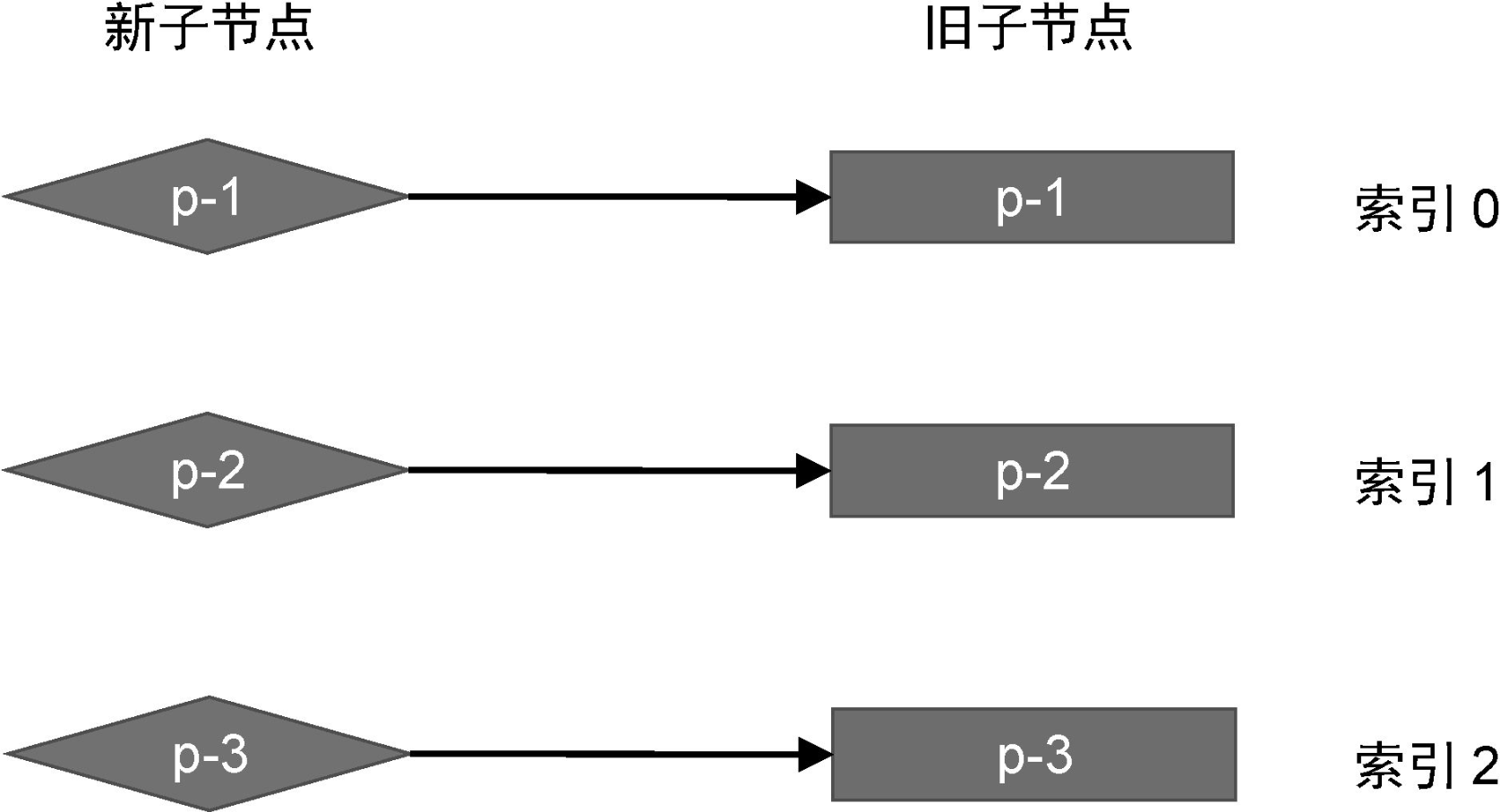
我们对新旧两组子节点采用上一节介绍的更新算法，看看当新旧两组子节点的顺序没有发生变化时，更新算法具有怎样的特点。

1、取新的一组子节点中的 p-1，它的 key 为 1。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 0。

2、取新的一组子节点中的 p-2，它的 key 为 2。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 1。

3、取新的一组子节点中的 p-3，它的 key 为 3。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 2。

在这个过程中，每一次寻找可复用的节点时，都会记录该可复用节点在旧的一组子节点中的位置索引。如果把这些位置索引值按照先后顺序排列，则可以得到一个序列：0、1、2。这是一个递增的序列，在这种情况下不需要移动任何节点。

# 新旧子节点顺序改变

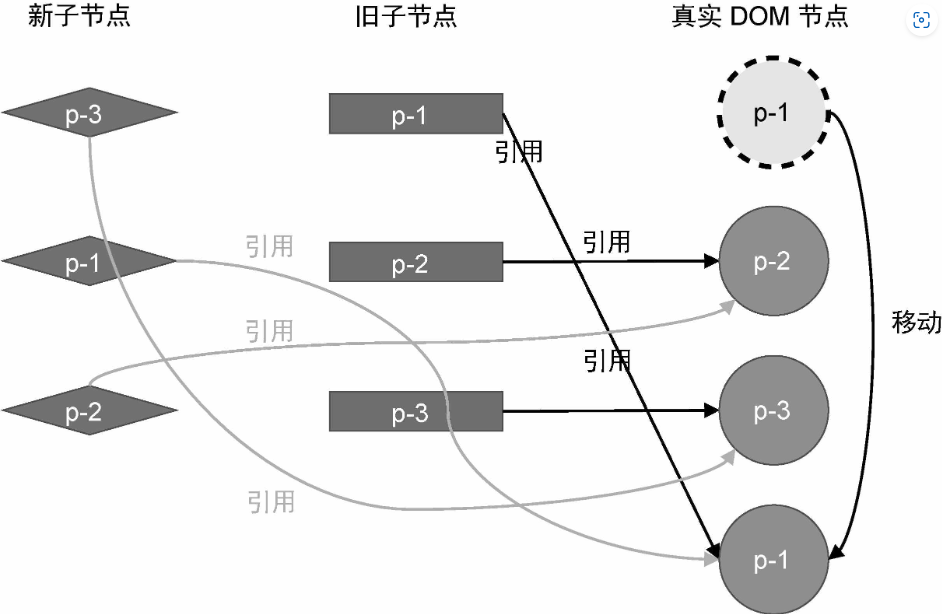
我们再来看看一个新旧子节点顺序改变的例子：

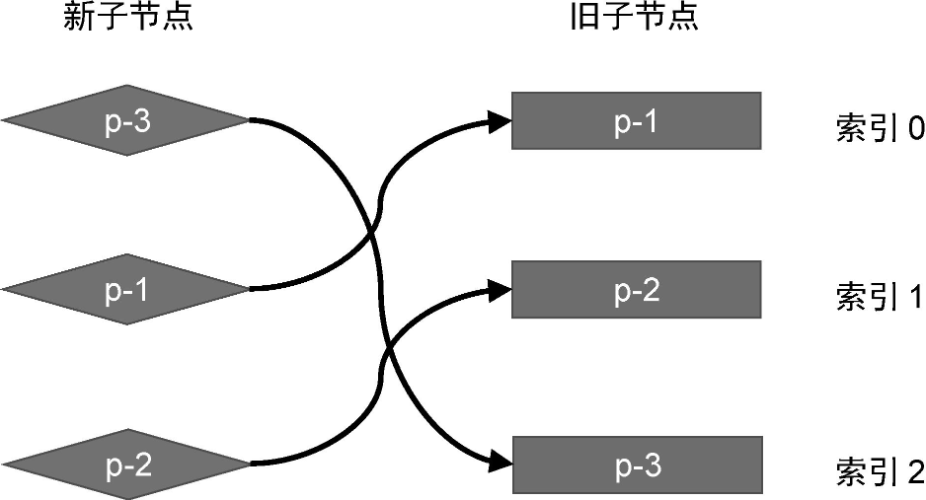
我们再次执行更新算法，看看这一次会有什么不同。

1、取新的一组子节点中的 p-3，它的 key 为 3。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 2。

2、取新的一组子节点中的 p-1，它的 key 为 1。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 0。

到了这一步我们发现，索引值递增的顺序被打破了。节点 p-1 在旧 children 中的索引是 0，它小于节点 p-3 在旧 children 中的索引 2。这说明节点 p-1 在旧 children中排在节点 p-3 前面，但在新的 children 中，它排在节点 p-3 后面。因此，我们能够得出一个结论：节点 p-1 对应的真实 DOM 需要移动。

3、取新的一组子节点中的 p-2，它的 key 为 2。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点，发现能够找到，并且该节点在旧的一组子节点中的索引为 1。

到了这一步我们发现，节点 p-2 在旧 children 中的索引 1 要小于节点 p-3 在旧children 中的索引 2。这说明，节点 p-2 在旧 children 中排在节点 p-3 前面，但在新的 children 中，它排在节点 p-3 后面。因此，节点 p-2 对应的真实 DOM 也需要移动。

以上就是 Diff 算法在执行更新的过程中，判断节点是否需要移动的方式。在上面的例子中，我们得出了节点 p-1 和节点 p-2 需要移动的结论。这是因为它们在旧children 中的索引要小于节点 p-3 在旧 children 中的索引。如果我们按照先后顺序记录在寻找节点过程中所遇到的位置索引，将会得到序列：2、0、1。可以发现，这个序列不具有递增的趋势。

其实我们可以将节点 p-3 在旧 children 中的索引定义为：在旧 children 中寻找具有相同 key 值节点的过程中，遇到的最大索引值。如果在后续寻找的过程中，存在索引值比当前遇到的最大索引值还要小的节点，则意味着该节点需要移动。

我们可以用 lastIndex 变量存储整个寻找过程中遇到的最大索引值：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     // 用来存储寻找过程中遇到的最大索引值
     let lastIndex = 0
     for (let i = 0; i < newChildren.length; i++) {
       const newVNode = newChildren[i]
       for (let j = 0; j < oldChildren.length; j++) {
         const oldVNode = oldChildren[j]
         if (newVNode.key === oldVNode.key) {
           patch(oldVNode, newVNode, container)
           if (j < lastIndex) {
             // 如果当前找到的节点在旧 children 中的索引小于最大索引值 lastIndex，
             // 说明该节点对应的真实 DOM 需要移动
           } else {
             // 如果当前找到的节点在旧 children 中的索引不小于最大索引值，
             // 则更新 lastIndex 的值
             lastIndex = j
           }
           break // 这里需要 break
         }
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

如果新旧节点的 key 值相同，说明我们在旧 children 中找到了可复用 DOM 的节点。

此时我们用该节点在旧 children 中的索引 j 与 lastIndex进行比较，如果 j 小于 lastIndex，说明当前 oldVNode 对应的真实 DOM 需要移动，否则说明不需要移动。

但此时应该将变量 j 的值赋给变量 lastIndex，以保证寻找节点的过程中，变量 lastIndex 始终存储着当前遇到的最大索引值。

lastlndex 存储的是旧索引组成的递增序列中的最大值，如果后续出现打破递增序列的索引（即索引小于lastlndex），则意味这这个索引对应的节点需要往后移动。

简单理解就是原来在旧 children 中，这个节点索引小于 lastlndex ，说明其原来是排在 lastlndex 对应的节点前面的，但是现在是排在后面（按顺序遍历），所以应该要把它往后移动。

# 如何移动元素

移动节点：指的是移动一个虚拟节点所对应的真实 DOM 节点，并不是移动虚拟节点本身。既然移动的是真实 DOM 节点，那么就需要取得对它的引用才行。

我们知道，当一个虚拟节点被挂载后，其对应的真实 DOM 节点会存储在它的 vnode.el 属性中：

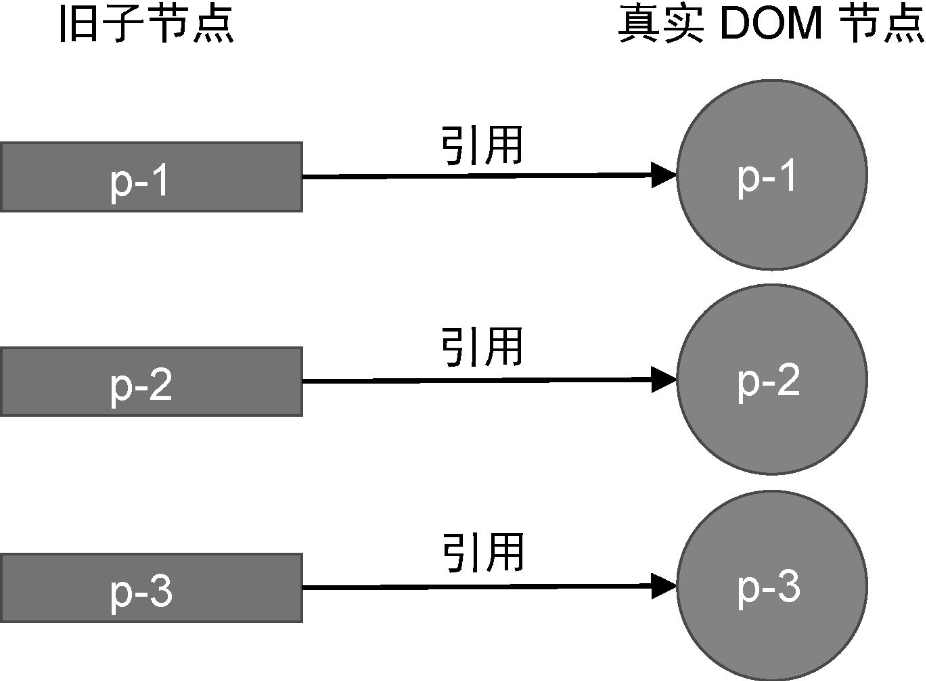
因此，在代码中，我们可以通过旧子节点的 vnode.el 属性取得它对应的真实 DOM 节点。

当更新操作发生时，渲染器会调用 patchElement 函数在新旧虚拟节点之间进行打补丁。回顾一下 patchElement 函数的代码：

 function patchElement(n1, n2) {
   // 新的 vnode 也引用了真实 DOM 元素
   const el = n2.el = n1.el
   // 省略部分代码
 }

1
2
3
4
5

可以看到，patchElement 函数首先将旧节点的 n1.el 属性赋值给新节点的 n2.el 属性。这个赋值语句的真正含义其实就是 DOM 元素的复用。

在复用了 DOM 元素之后，新节点也将持有对真实 DOM 的引用：

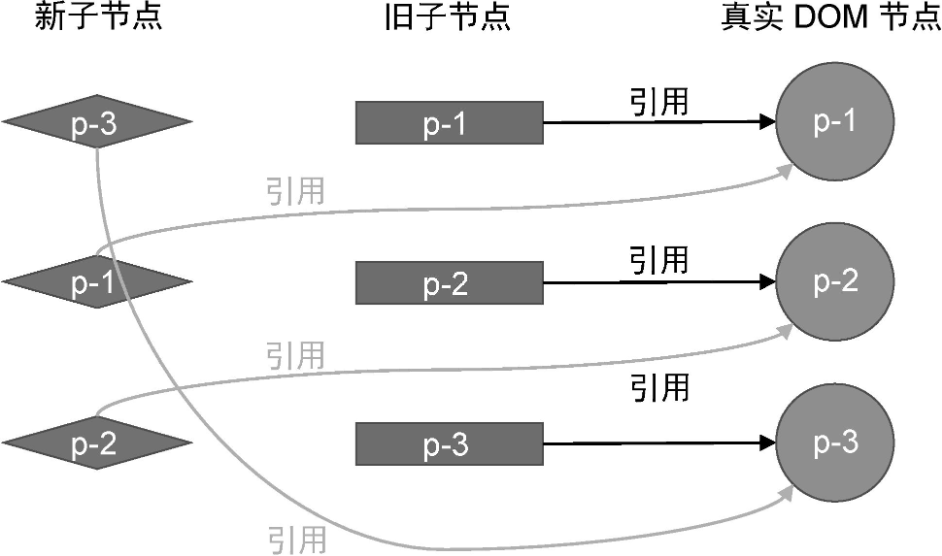
可以看到，无论是新子节点还是旧子节点，都存在对真实 DOM 的引用，在此基础上，我们就可以进行 DOM 移动操作了。

新的虚拟节点其实就是真实的新顺序，所以当出现索引降序需要移动节点时，只要参考新节点数组中前一个节点的 el 进行移动即可（移动到它后面，如果没有前一个节点，说明不要移动）。

为了阐述具体应该怎样移动 DOM 节点，我们仍然引用上一节的更新案例：

它的更新步骤如下：

1、取新的一组子节点中的 p-3，它的 key 为 3，可复用节点在旧的一组子节点中的索引为 2。此时变量 lastIndex 的值为 0，索引 2 不小于 0，所以节点 p-3 对应的真实 DOM 不需要移动，但需要更新变量 lastIndex 的值为 2。

2、取新的一组子节点中的 p-1，它的 key 为 1，可复用节点在旧的一组子节点中的索引为 0。此时变量 lastIndex 的值为 2，索引 0 小于 2，所以节点 p-1 对应的真实 DOM 需要移动。

到了这一步，我们发现，节点 p-1 对应的真实 DOM 需要移动，但应该移动到哪里呢？我们知道，新 children 的顺序其实就是更新后真实 DOM 节点应有的顺序。所以节点 p-1 在新 children 中的位置就代表了真实 DOM 更新后的位置。由于节点 p-1在新 children 中排在节点 p-3 后面，所以我们应该把节点 p-1 所对应的真实 DOM移动到节点 p-3 所对应的真实 DOM 后面。移动后的结果如图所示：

可以看到，这样操作之后，此时真实 DOM 的顺序为 p-2、p-3、p-1。

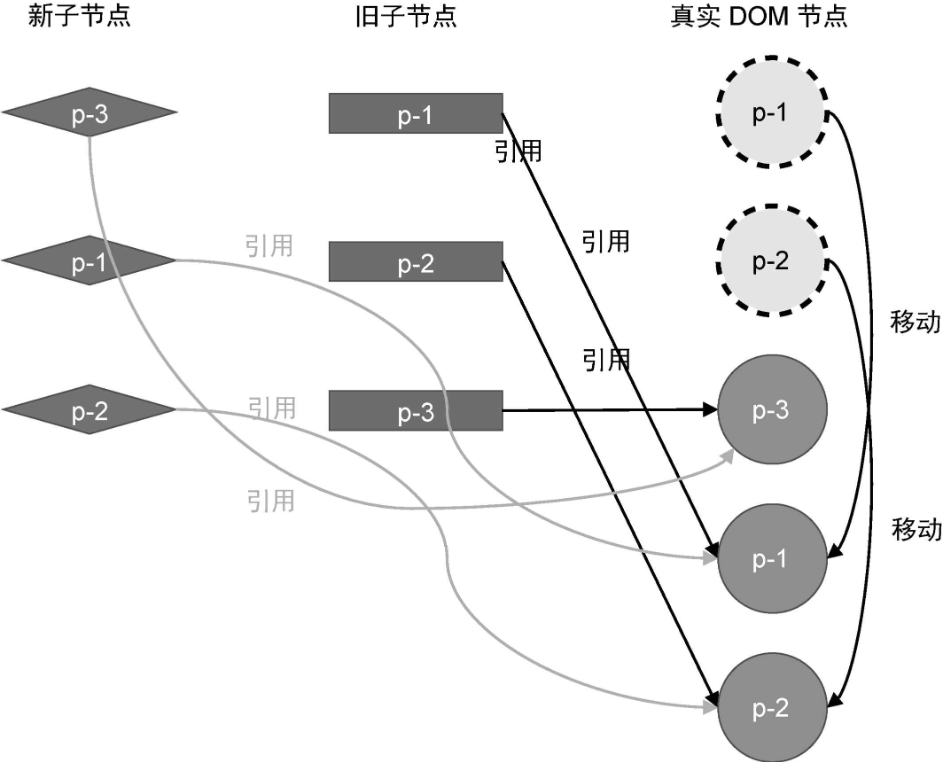
3、取新的一组子节点中的 p-2，它的 key 为 2，可复用节点在旧的一组子节点中的索引为 1。此时变量 lastIndex 的值为 2，索引 1 小于 2，所以节点 p-2 对应的真实 DOM 需要移动。

第三步与第二步类似，节点 p-2 对应的真实 DOM 也需要移动。同样，由于节点 p-2在新 children 中排在节点 p-1 后面，所以我们应该把节点 p-2 对应的真实 DOM 移动到节点 p-1 对应的真实 DOM 后面。移动后的结果如图所示：

经过这一步移动操作之后，我们发现，真实 DOM 的顺序与新的一组子节点的顺序相同了：p-3、p-1、p-2。至此，更新操作完成。

接下来，我们着手实现代码。其实并不复杂，如下面 patchChildren 函数的代码所示：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     let lastIndex = 0
     for (let i = 0; i < newChildren.length; i++) {
       const newVNode = newChildren[i]
       let j = 0
       for (j; j < oldChildren.length; j++) {
         const oldVNode = oldChildren[j]
         if (newVNode.key === oldVNode.key) {
           patch(oldVNode, newVNode, container)
           if (j < lastIndex) {
             // 代码运行到这里，说明 newVNode 对应的真实 DOM 需要移动
             // 先获取 newVNode 的前一个 vnode，即 prevVNode
             const prevVNode = newChildren[i - 1]
             // 如果 prevVNode 不存在，则说明当前 newVNode 是第一个节点，它不需要移动
             if (prevVNode) {
               // 由于我们要将 newVNode 对应的真实 DOM 移动到 prevVNode 所对应真实 DOM 后面，
               // 所以我们需要获取 prevVNode 所对应真实 DOM 的下一个兄弟节点，并将其作为锚点
               const anchor = prevVNode.el.nextSibling
               // 调用 insert 方法将 newVNode 对应的真实 DOM 插入到锚点元素前面，
               // 也就是 prevVNode 对应真实 DOM 的后面
               insert(newVNode.el, container, anchor)
             }
           } else {
             lastIndex = j
           }
           break
         }
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

如果条件 j < lastIndex 成立，则说明当前 newVNode 所对应的真实 DOM 需要移动。

思路：我需要移动、则需要知道我的上一个是谁，也就是 newChildren[i - 1]，然后插入。

根据前文的分析可知，我们需要获取当前 newVNode 节点的前一个虚拟节点，即 newChildren[i - 1]，然后使用 insert 函数完成节点的移动，其中 insert 函数依赖浏览器原生的 insertBefore 函数：

 const renderer = createRenderer({
   // 省略部分代码
   insert(el, parent, anchor = null) {
     // insertBefore 需要锚点元素 anchor
     parent.insertBefore(el, anchor)
   }
   // 省略部分代码
 })

1
2
3
4
5
6
7
8

# 添加新元素

如图所示：

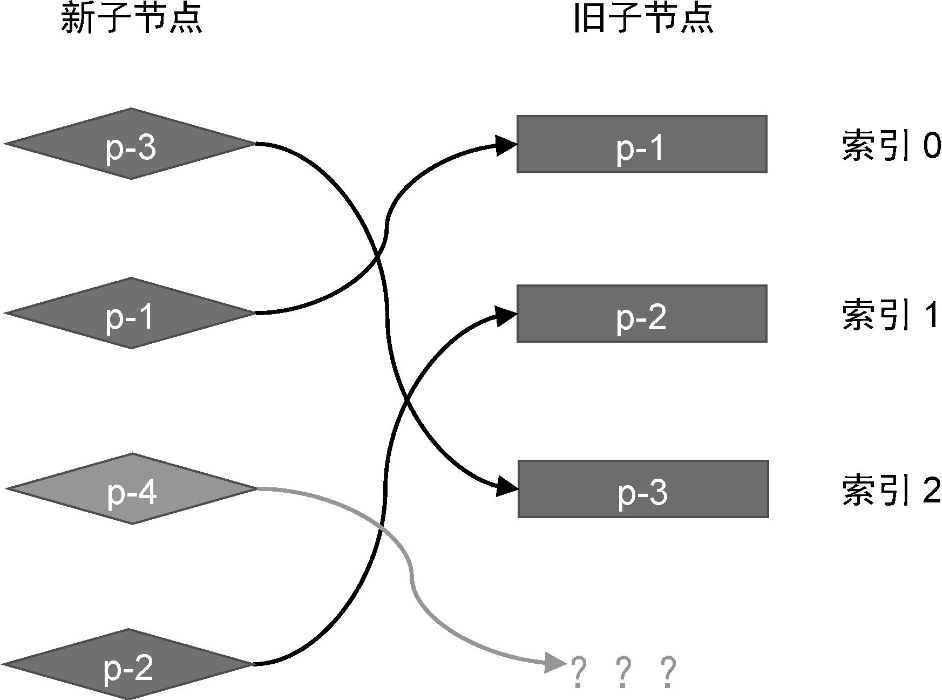
添加新元素

在新的一组子节点中，多出来一个节点 p-4，它的 key 值为 4，该节点在旧的一组子节点不存在，因此应该将其视为新增节点。对于新增节点，在更新时我们应该正确地将它挂载，这主要分为两步：

想办法找到新增节点；
将新增节点挂载到正确位置。

为了搞清楚如何找到新增节点这个问题，我们需要根据上图中给出的例子，模拟执行简单 Diff 算法的逻辑。在此之前，我们需要弄清楚新旧两组子节点与真实 DOM 元素的当前状态：

两组子节点与真实DOM元素的当前状态

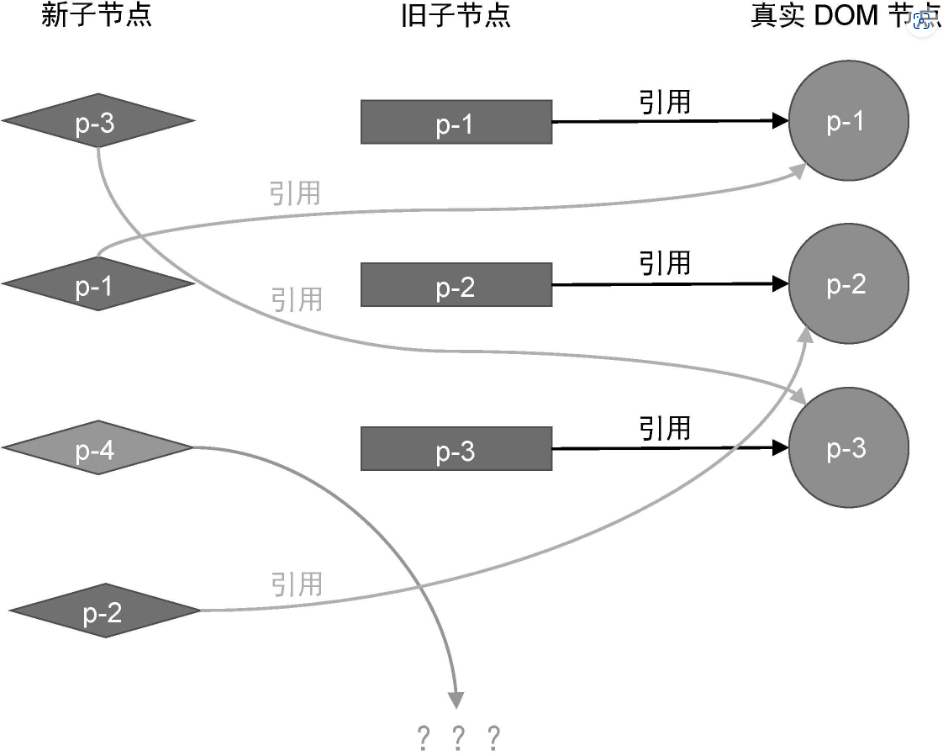
接着，我们开始模拟执行简单 Diff 算法的更新逻辑。

1、取新的一组子节点中的 p-3，它的 key 值为 3，可复用节点在旧的一组子节点中的索引值为 2。此时，变量 lastIndex 的值为 0，索引值 2 不小于 lastIndex 的值 0，所以节点 p-3 对应的真实 DOM 不需要移动，但是需要将变量 lastIndex 的值更新为 2。

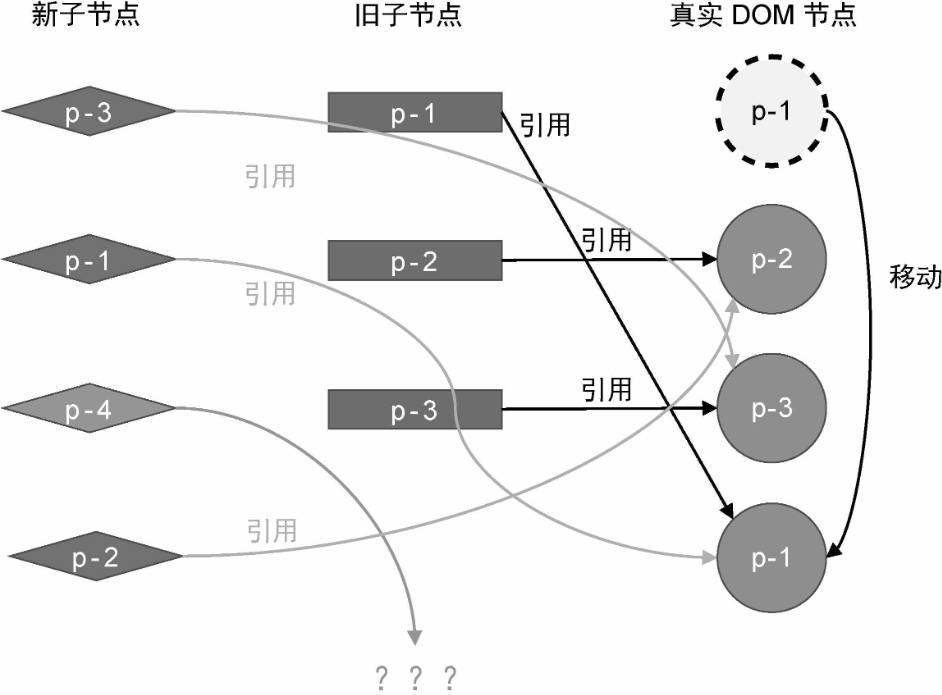
2、取新的一组子节点中的 p-1，它的 key 值为 1，可复用节点在旧的一组子节点中的索引值为 0。此时变量 lastIndex 的值为 2，索引值 0 小于 lastIndex 的值 2，所以节点 p-1 对应的真实 DOM 需要移动，并且应该移动到节点 p-3 对应的真实 DOM 后面。经过这一步的移动操作后，真实 DOM 的状态如图所示：

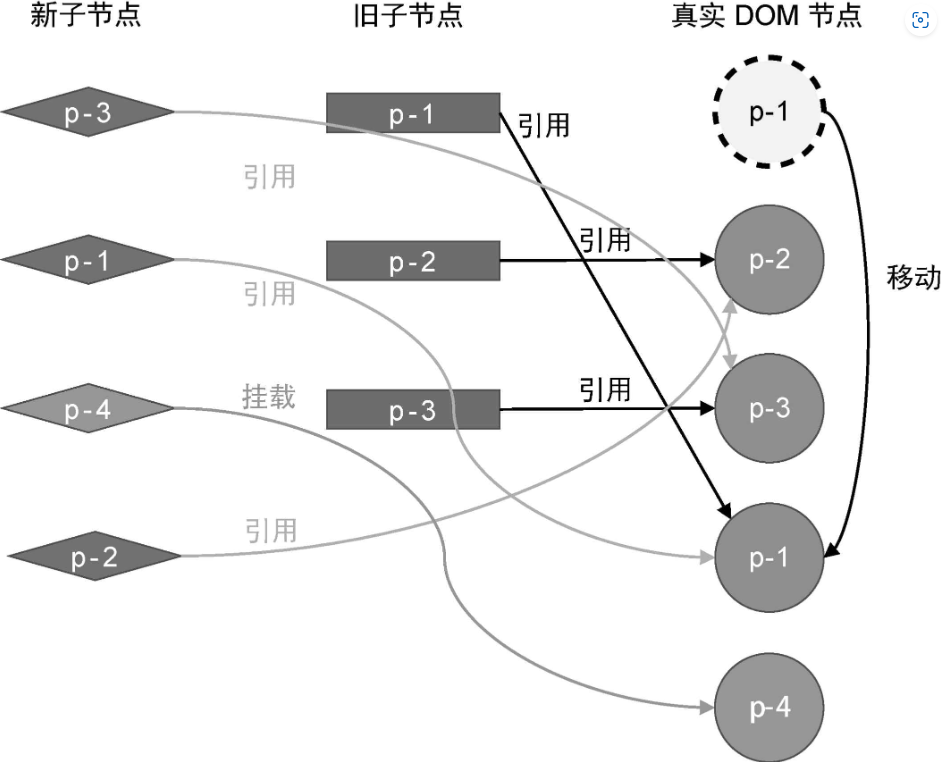
此时真实 DOM 的顺序为 p-2、p-3、p-1。

3、取新的一组子节点中的 p-4，它的 key 值为 4，由于在旧的一组子节点中，没有 key 值为 4 的节点，因此渲染器会把节点 p-4 看作新增节点并挂载它。那么，应该将它挂载到哪里呢？为了搞清楚这个问题，我们需要观察节点 p-4 在新的一组子节点中的位置。由于节点 p-4 出现在节点 p-1 后面，所以我们应该把节点 p-4 挂载到节点 p-1 所对应的真实 DOM 后面。在经过这一步挂载操作之后，真实 DOM 的状态如图所示：

此时真实 DOM 的顺序是：p-2、p-3、p-1、p-4，其中 p-4 是刚刚挂载的。

4、取新的一组子节点中的p-2，它的 key 值为 2，可复用节点在旧的一组子节点中的索引值为1。此时变量 lastIndex 的值为 2，索引值 1 小于 lastIndex 的值 2，所以节点 p-2 对应的真实 DOM 需要移动，并且应该移动到节点 p-4 对应的真实 DOM 后面。经过这一步移动操作后，真实 DOM 的状态如图所示：

此时真实 DOM 的顺序是：p-3、p-1、p-4、p-2。

至此，真实 DOM 的顺序已经与新的一组子节点的顺序相同了，更新完成。

接下来，我们着手实现代码，如下面 patchChildren 函数的代码所示：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     let lastIndex = 0
     for (let i = 0; i < newChildren.length; i++) {
       const newVNode = newChildren[i]
       let j = 0
       // 在第一层循环中定义变量 find，代表是否在旧的一组子节点中找到可复用的节点，
       // 初始值为 false，代表没找到
       let find = false
       for (j; j < oldChildren.length; j++) {
         const oldVNode = oldChildren[j]
         if (newVNode.key === oldVNode.key) {
           // 一旦找到可复用的节点，则将变量 find 的值设为 true
           find = true
           patch(oldVNode, newVNode, container)
           if (j < lastIndex) {
             const prevVNode = newChildren[i - 1]
             if (prevVNode) {
               const anchor = prevVNode.el.nextSibling
               insert(newVNode.el, container, anchor)
             }
           } else {
             lastIndex = j
           }
           break
         }
       }
       // 如果代码运行到这里，find 仍然为 false，
       // 说明当前 newVNode 没有在旧的一组子节点中找到可复用的节点
       // 也就是说，当前 newVNode 是新增节点，需要挂载
       if (!find) {
         // 为了将节点挂载到正确位置，我们需要先获取锚点元素
         // 首先获取当前 newVNode 的前一个 vnode 节点
         const prevVNode = newChildren[i - 1]
         let anchor = null
         if (prevVNode) {
           // 如果有前一个 vnode 节点，则使用它的下一个兄弟节点作为锚点元素
           anchor = prevVNode.el.nextSibling
         } else {
           // 如果没有前一个 vnode 节点，说明即将挂载的新节点是第一个子节点
           // 这时我们使用容器元素的 firstChild 作为锚点
           anchor = container.firstChild
         }
         // 挂载 newVNode
         patch(null, newVNode, container, anchor)
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

找了一轮没找到相同的 key，说明是需要新插入的节点，这个时候看自己的位置，如果不是第一个位置就参照前序节点 el 的 nextsibling；如果是第一个位置，就用 container.firstChild 找到参照位置。最后插入的操作都是 insert（ insert 封装了/依赖于浏览器原生的 insertBefore 函数）。

首先，我们在外层循环中定义了名为 find 的变量，它代表渲染器能否在旧的一组子节点中找到可复用的节点。变量 find 的初始值为 false，一旦寻找到可复用的节点，则将变量 find 的值设置为 true。如果内层循环结束后，变量 find 的值仍然为 false，则说明当前 newVNode 是一个全新的节点，需要挂载它。
为了将节点挂载到正确位置，我们需要先获取锚点元素：找到 newVNode 的前一个虚拟节点，即 prevVNode，如果存在，则使用它对应的真实 DOM 的下一个兄弟节点作为锚点元素；如果不存在，则说明即将挂载的 newVNode 节点是容器元素的第一个子节点，此时应该使用容器元素的 container.firstChild 作为锚点元素。
最后，将锚点元素anchor 作为 patch 函数的第四个参数，调用 patch 函数完成节点的挂载。但由于目前实现的 patch 函数还不支持传递第四个参数，所以我们需要调整 patch 函数的代码。

但由于目前实现的 patch 函数还不支持传递第四个参数，所以我们需要调整 patch 函数的代码：

 // patch 函数需要接收第四个参数，即锚点元素
 function patch(n1, n2, container, anchor) {
   // 省略部分代码

   if (typeof type === 'string') {
     if (!n1) {
       // 挂载时将锚点元素作为第三个参数传递给 mountElement 函数
       mountElement(n2, container, anchor)
     } else {
       patchElement(n1, n2)
     }
   } else if (type === Text) {
     // 省略部分代码
   } else if (type === Fragment) {
     // 省略部分代码
   }
 }
 // mountElement 函数需要增加第三个参数，即锚点元素
 function mountElement(vnode, container, anchor) {
   // 省略部分代码
   // 在插入节点时，将锚点元素透传给 insert 函数
   insert(el, container, anchor)
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 移除不存在的元素

在更新子节点时，不仅会遇到新增元素，还会出现元素被删除的情况：

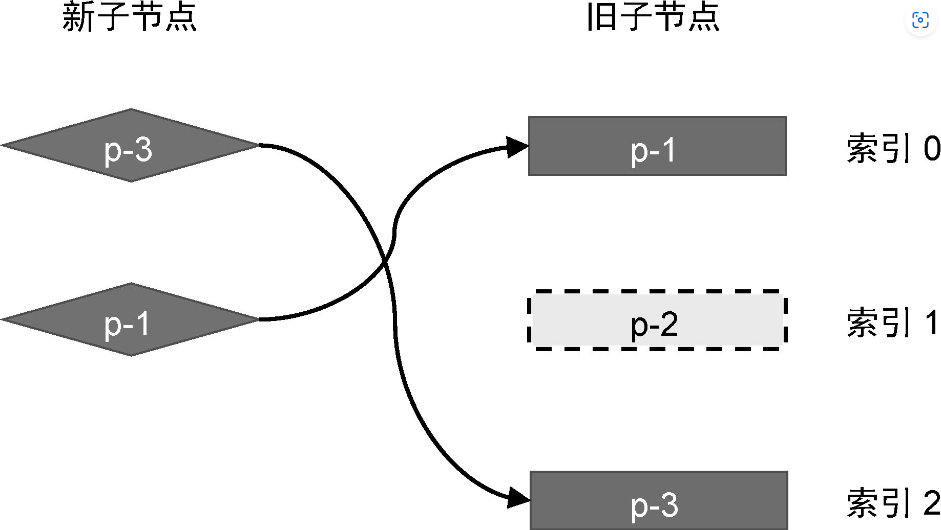
移除不存在的元素

在新的一组子节点中，节点 p-2 已经不存在了，这说明该节点被删除了。渲染器应该能找到那些需要删除的节点并正确地将其删除。

如何找到需要删除的节点呢？以上图为例，我们来分析它的更新步骤。在模拟执行更新逻辑之前，我们需要清楚新旧两组子节点以及真实 DOM 节点的当前状态：

当前状态

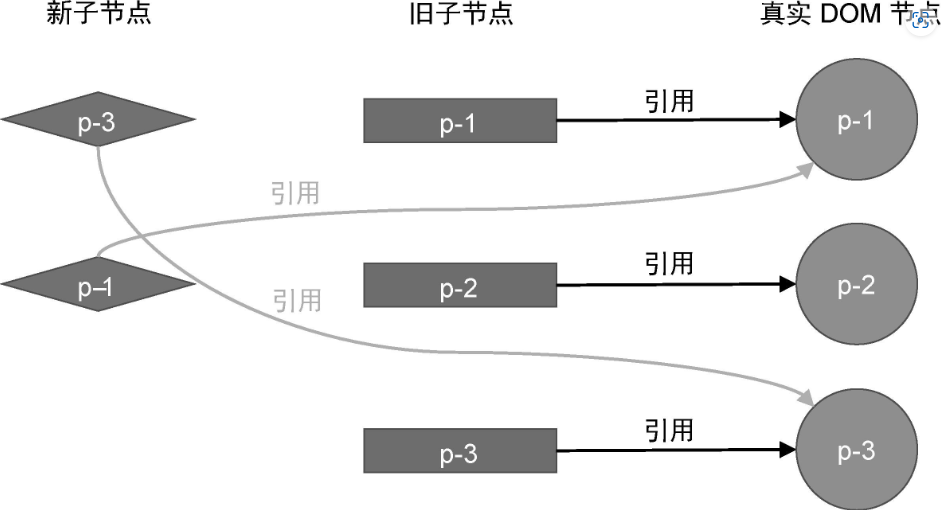
接着，我们开始模拟执行更新的过程。

1、取新的一组子节点中的 p-3，它的 key 值为 3，可复用节点在旧的一组子节点中的索引值为 2。此时变量 lastIndex 的值为 0，索引 2 不小于 lastIndex 的值 0，所以节点 p-3对应的真实 DOM 不需要移动，但需要更新变量 lastIndex 的值为 2。

2、取新的一组子节点中的 p-1，它的 key 值为 1，可复用节点在旧的一组子节点中的索引值为 0。此时变量 lastIndex 的值为 2，索引 0 小于 lastIndex 的值 2，所以节点 p-1 对应的真实 DOM 需要移动，并且应该移动到节点 p-3 对应的真实 DOM 后面。经过这一步的移动操作后，真实 DOM 的状态如图所示：

至此，更新结束。

我们发现，节点 p-2 对应的真实 DOM 仍然存在，所以需要增加额外的逻辑来删除遗留节点。思路很简单，当基本的更新结束时，我们需要遍历旧的一组子节点，然后去新的一组子节点中寻找具有相同 key 值的节点。如果找不到，则说明应该删除该节点，如下面 patchChildren 函数的代码所示：

 function patchChildren(n1, n2, container) {
   if (typeof n2.children === 'string') {
     // 省略部分代码
   } else if (Array.isArray(n2.children)) {
     const oldChildren = n1.children
     const newChildren = n2.children
     let lastIndex = 0
     for (let i = 0; i < newChildren.length; i++) {
       // 省略部分代码
     }
     // 上一步的更新操作完成后
     // 遍历旧的一组子节点
     for (let i = 0; i < oldChildren.length; i++) {
       const oldVNode = oldChildren[i]
       // 拿旧子节点 oldVNode 去新的一组子节点中寻找具有相同 key 值的节点
       const has = newChildren.find(
         vnode => vnode.key === oldVNode.key
       )
       if (!has) {
         // 如果没有找到具有相同 key 值的节点，则说明需要删除该节点
         // 调用 unmount 函数将其卸载
         unmount(oldVNode)
       }
     }
   } else {
     // 省略部分代码
   }
 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

在上一步的更新操作完成之后，我们还需要遍历旧的一组子节点，目的是检查旧子节点在新的一组子节点中是否仍然存在，如果已经不存在了，则调用 unmount 函数将其卸载。

因为上一轮循环的外循环是以 newChildren 为目标循环的，不能照顾到旧节点中被删的部分。所以在结束后需要再用一个循环检查被删除的部分，执行 unmount 逻辑。

# 总结

Diff 算法用来计算两组子节点的差异，并试图最大程度地复用 DOM 元素。
采用一种简单的方式来更新子节点，即卸载所有旧子节点，再挂载所有新子节点。然而这种更新方式无法对 DOM元素进行复用，需要大量的 DOM 操作才能完成更新，非常消耗性能。
改进后的方案是，遍历新旧两组子节点中数量较少的那一组，并逐个调用 patch 函数进行打补丁，然后比较新旧两组子节点的数量，如果新的一组子节点数量更多，说明有新子节点需要挂载；否则说明在旧的一组子节点中，有节点需要卸载。
虚拟节点中 key 属性的作用：它就像虚拟节点的“身份证号”。在更新时，渲染器通过 key 属性找到可复用的节点，然后尽可能地通过 DOM 移动操作来完成更新，避免过多地对 DOM 元素进行销毁和重建。
简单 Diff 算法的核心逻辑是，拿新的一组子节点中的节点去旧的一组子节点中寻找可复用的节点。如果找到了，则记录该节点的位置索引。我们把这个位置索引称为最大索引。在整个更新过程中，如果一个节点的索引值小于最大索引，则说明该节点对应的真实 DOM 元素需要移动。

新增：新节点组从上往下遍历，嵌套遍历旧节点，通过 key 在找到对应的旧节点，找不到则新增节点。

移动：找到旧节点后用旧索引比对 max 旧索引，如果比 max 还要大，则覆盖；反之则需要移动（因为是上往下遍历，所以当前的节点的新索引肯定比前面节点的新索引大，而此刻旧索引对比结果却相反，说明当前节点需要移动），则移动节点（移动元素其实只有一个原则，移动到前一个节点的后面，如果自己是第一个则不动）

删除：遍历旧节点组，嵌套遍历新节点组，通过 key 寻找对应新节点，找不到则删除。

8.挂载与更新 10.双端Diff算法

Vivien's Notebook

Choose mode